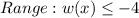Solution:
Given:
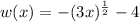
Rewriting the function, by applying the law of fractional exponents,
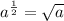
Hence,
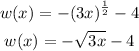
The domain of a function is the set of all input values that make the function defined.
The function is undefined when the value of x under the root sign is less than zero because the square root of a negative number is complex.
Hence, the domain exists when x has a value greater than or equal to 0.
Therefore, the domain is;
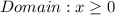
The range of a function is the set of all output values that makes the function defined.
Hence, the range exists when y is lesser than or equal to minus 4 because a value of y greater than -4, makes the function and domain undefined.
Therefore, the range is;