ANSWER
B. 2.9 m
Step-by-step explanation
Let's draw the slide with the given information,
As we can see, the slide forms a right triangle with the ground. The length of the slide is the hypotenuse of the triangle and its height is the opposite leg to the given angle.
We have to use a trigonometric ratio to solve this problem and, with the given information, the one that best fits is the sine of the angle since it is the ratio between the opposite leg and the hypotenuse,
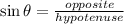
In this problem, the angle is 35°, the opposite leg is h and the hypotenuse is 5.1m,

Solving for h,
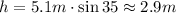
Hence, the height of the top of the slide is 2.9 m, rounded to the nearest tenth.