Question

Two 4.72 kg masses are 3.12 m apart on a frictionless table. Each has 85.5 microCoulombs of charge. What is the initial acceleration of each mass if they are released and allowed to move?

Answer 1

We are given the following information

Mass of objects: m = 4.72 kg

Distance between objects: r = 3.12 m

Charge: q = 85.5 μC

We are asked to find the initial acceleration of each mass.

Recall from Newton's second law of motion,

`F=m\cdot a`

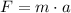
Where F is the force between two masses, m is the mass, and a is the acceleration.

First, let us find the force between the two masses.

Recall from Coulomb's law,

`F=(k\cdot q_1\cdot q_2)/(r^2)`

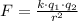
Where k is the Coulomb's law constant that is k = 9×10⁹ Nm²/C²

Substitute the given values into the above formula

`\begin{gathered} F=(9*10^9\cdot85.5*10^(-6)\cdot85.5*10^(-6))/(3.12^2) \\ F=6.7587\;N \end{gathered}`

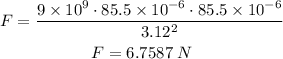
Finally, the initial acceleration of each mass is

`\begin{gathered} F=m\cdot a \\ a=(F)/(m) \\ a=(6.7587)/(4.72) \\ a=1.43\;(m)/(s^2) \end{gathered}`

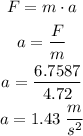
Therefore, the initial acceleration of each mass is 1.43 m/s^2