Question

Can I have this practice problem answered, I will provide the answer options in another picture

Answer 1

Given the equation of the parabola as;

`(y+1)^2=12(x-3)`

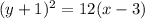
The standard equation of a parabola with vertex (h,k) and focus |p| is;

`(y-k)^2=4p(x-h)`

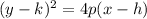
Relating this equation to the given equation of the parabola, we got the vertex as;

`\begin{gathered} x-h=x-3 \\ h=3 \\ \text{and} \\ y-k=y+1 \\ k=-1 \\ (h,k)=(3,-1) \end{gathered}`

Thus, the vertex of the parabola is (3, -1)

The graph of the parabola is;

The parabola opens right.

Parabola is symmetric around the x-axis, so the focus lies a distance p from the centre (3,-1) along the x-axis.

`\begin{gathered} (3+p,-1) \\ \text{Where p=3;} \\ \text{focus}=(6,-1) \end{gathered}`

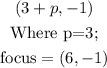
From the graph, the focus is 3units away from the vertex.

Parabola is symmetric around the x-axis and so the directrix is a line parallel to the y-axis. Thus, the directrix of the equation is;

`\begin{gathered} x=3-p \\ x=3-3 \\ x=0 \end{gathered}`

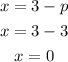
From the graph, the directrix is 6units from the focus.

The focus is the point (6,-1)

The directrix of the equation is x=0