Let:
• y, be the cost of the plan
,
• x, be the minutes spend on call
This way, we'll have:
Plan A:
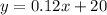
Plan B:
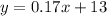
If the two plans cost the same, we'll have that:
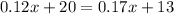
Solving for x :
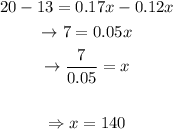
A) The two plans will cost the same for 140 minutes on call
The cost will be:
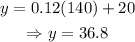
B) $36.80