The equal sides of an isosceles triangle are known as the 'legs. ' The third and unequal side of an isosceles triangle is known as the 'base The angles situated opposite to the equal sides of an isosceles triangle are always equal.
The given values in the question are
![\begin{gathered} \text{Vertex angle =}48^0 \\ Length\text{ of the legs=}14\operatorname{cm} \end{gathered}]()
The base angles are equal to each other
![\begin{gathered} \angle A=48^0 \\ \angle B=x \\ \angle C=x \\ a=\text{?} \\ b=14\operatorname{cm} \\ c=14\operatorname{cm} \end{gathered}]()
a) The measure of the base angles
The sum of angles in a triangle is = 180°
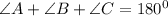
By substituting the values, we will have

The measure of the base angles are 66° each
b)The area of the triangle Where two sides and angle give we will use the formula below
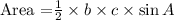
By substituting the values, we will have
![\begin{gathered} \text{Area =}(1)/(2)* b* c*\sin A \\ \text{Area}=(1)/(2)*14\operatorname{cm}*14\operatorname{cm}*\sin 48^0 \\ \text{Area}=7\operatorname{cm}*14\operatorname{cm}*\sin 48^0 \\ \text{Area}=72.83\operatorname{cm}^2 \end{gathered}]()
The Area of the triangle is = 72.83cm²
c) The perimeter:
The perimeter of the triangle can be calculated using the formula below
![\begin{gathered} \text{Perimeter}=a+b+c \\ \text{Perimeter}=a+14\operatorname{cm}+14cm \end{gathered}]()
First, we will have to calculate the value of a using Sine Rule
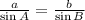
By substituting the values, we will have
![\begin{gathered} (a)/(\sin A)=(b)/(\sin B) \\ (a)/(\sin 48^0)=(14)/(\sin 66^0) \\ \text{Cross multiply} \\ a*\sin 66^0=14*\sin 48^0 \\ a=(14*\sin 48^0)/(\sin 66) \\ a=11.38\operatorname{cm} \\ a=11.4\operatorname{cm} \end{gathered}]()
Substitute the value of a in the formula for the perimeter
![\begin{gathered} \text{Perimeter}=a+14\operatorname{cm}+14cm \\ \text{Perimeter}=11.4\operatorname{cm}+14cn+14\operatorname{cm} \\ \text{Perimeter}=39.4\operatorname{cm} \end{gathered}]()
Therefore,
The perimeter of the triangle is = 39.4cm