In order to find the factors of this polynomial, let's first make it equal 0, solve it using the quadratic formula to find the zeros and then write it in the factored form:
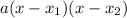
So we have:
![\begin{gathered} 30x^2-33x+3=0 \\ a=30,b=-33,c=3 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_1=\frac{33+\sqrt[]{1089-4\cdot30\cdot3}}{2\cdot30}=(33+27)/(60)=1 \\ x_2=(33-27)/(60)=(6)/(60)=(1)/(10) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2psmiti25dyiuvk7c0d10ydb9ehqig7y0h.png)
Then, the factored form is:
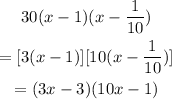
Therefore one of the factors is 10x - 1 and the correct option is the fourth one.