hello
to solve this problem, we have to use the formula of volume of a hemisphere
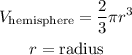
in this question, we are given the value of diameter, we have to use this information to find the radius of the hemisphere
![\begin{gathered} \text{radius}=\frac{\text{diameter}}{2} \\ \text{diameter}=24\operatorname{cm} \\ \text{radius}=(24)/(2) \\ \text{radius}=12\operatorname{cm} \end{gathered}]()
let's proceed and insert the value of the radius into the formula above
![\begin{gathered} V_{\text{hemisphere}}=(2)/(3)\pi r^3 \\ r=12\operatorname{cm} \\ V_{\text{hemisphere}}=(2)/(3)*\pi*12^3 \\ V_{\text{hemisphere}}=(2)/(3)*1728*\pi \\ V_{\text{hemisphere}}=1152\pi cm^3 \end{gathered}]()
from the calculation above, the volume of the hemisphere is equal to 1152pi cm^3