Question

Which of the following are the equations for the line shown

Answer 1

Two points on the line are (-3,3) and (-1,-3)

The equation of a straight line given two points can be calculated by the formula

`\begin{gathered} (y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1) \\ \\ \text{Where (x}_1,y_1)=(-3,3)and(x_2,y_2)=(-1,-3) \end{gathered}`

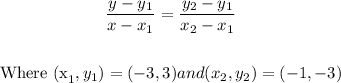
By substituting into the formula above, we have

`\begin{gathered} (y-3)/(x-(-3))=(-3-3)/(-1-(-3)) \\ (y-3)/(x+3)=(-6)/(-1+3) \\ (y-3)/(x+3)=(-6)/(2) \\ (y-3)/(x+3)=-3 \\ y-3=-3(x+3) \\ \end{gathered}`

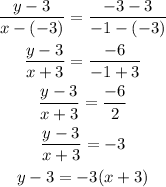
The first correct choice is y-3 = -3(x+3)

Looking at the options given, we can also write the equation in another form by adding 6 to both sides

`\begin{gathered} y-3=-3(x+3) \\ \text{add 6 to both sides} \\ y-3+6=-3(x+3)+6 \\ y+3=-3x-9+6 \\ y+3=-3x-3 \\ y+3=-3(x+1) \end{gathered}`

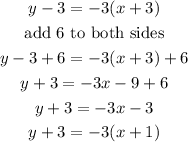
The second correct choice is y+3 = -3(x+1)

Hence, Option A and option B are the correct options