Solution:
Consider the following equation:
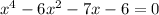
First, to solve this equation, we must factor it:
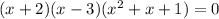
using the zero factor theorem, the following must be met:
Equation 1:
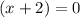
or
Equation 2:
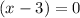
or
Equation 3:
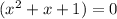
From equation 1, solving for x, we obtain:
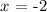
or from equation 2, solving for x, we obtain:
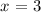
Now, remember the following quadratic formula to find the solutions of a quadratic equation:
![\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/kaoalb540qnvy45obw509ttuwfskx00e99.png)
applying this to equation 3, where
a = 1
b= 1
and
c = 1
we obtain:
![\frac{-1\pm\sqrt[]{1-4}}{2}=\frac{-1\pm\sqrt[]{-3}}{2}=\frac{-1\pm\sqrt[]{3}i\text{ }}{2}=-(1)/(2)\pm\frac{\sqrt[]{3}i\text{ }}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/f8xewxpmla90z2v6tmkdhgos3bd7ors4ll.png)
then, we obtain two additional solutions:
![-(1)/(2)+\frac{\sqrt[]{3}i\text{ }}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/t95hbevmx9b94tcbn0n9283emyoox8271y.png)
or
![-(1)/(2)-\frac{\sqrt[]{3}i\text{ }}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/jch9its6y2qst775bdpjicmrabgnmgtog7.png)
so that, we can conclude that the correct answer is:
The solutions (zeros) for the given equation are:
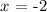
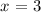
![-(1)/(2)+\frac{\sqrt[]{3}i\text{ }}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/t95hbevmx9b94tcbn0n9283emyoox8271y.png)
![-(1)/(2)-\frac{\sqrt[]{3}i\text{ }}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/jch9its6y2qst775bdpjicmrabgnmgtog7.png)