Question

Hello, I need some help with Part 2 question 5! Please show work as the instructions asked! I included other completed work from the assignment for extra information.

Answer 1

The given polynomial is:

`(x+7)(x-2)^2(x^2-4)(x+1)^4`

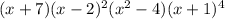
Using differece of squares, it follows:

`\begin{gathered} (x^2-4) \\ =\lparen x^2-2^2) \\ =(x-2)(x+2) \end{gathered}`

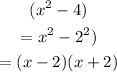
Substituting the expression into the given polynomial gives:

`(x+7)(x-2)^2(x-2)(x+2)(x+1)^4`

Thus the polynomial becomes:

`(x+7)(x-2)^3(x+2)(x+1)^4`

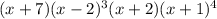
Using the Fundamental Theorem of Algebra the number of roots of the polynomial is equal to the degree of the polynomial.

Thus the number of roots is:

`1+3+1+4=9`

Therefore the number of roots is 9.

Notice that the factor with multiplicity of 3 is (x-2)

Therefore the code piece is E