Step-by-step explanation:
We are given the revenue function and the cost function for x units of a product as follows;
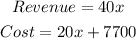
We are also told that to obtain a profit, the revenue must be higher than the cost. This means;
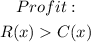
To determine which unit(s) of x will yield a profit, we can now substitute the values into the equation above;
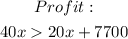
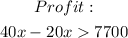
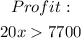
Divide both sides by 20;

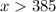
For this answer, we know that to make a profit, the units produced must be greater than 385 units.
ANSWER:
To obtain a profit the number of units must be greater than 385