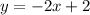Question

7. PT has a midpoint of U. The coordinate of point U isat (6,-2) and T is at (10,-10). What is the coordinateof the other endpoint, P?a. What is the coordinate of the other endpoint, P?bWhat is the length of PT?CWhat is the slope of PT?d. What is an equation for a line parallel to PT?

Answer 1

ANSWERS

a. Coodri (2, 6)

b. 8√5

c. -2

d. y = -2x + 2

Step-by-step explanation

a. To find the coordinate of point P we can do a diagram first that will help us see the problem more clearly:

U is the midpoint of segment PT, which means that the horizontal distance between U and T is the same as between P and U, but in the opposite direction (in this case to the left of U). The same happens to the vertical distance. Therefore, we have that the horizontal distance is:

`x_T-x_U=10-6=4_{}`

Therefore the x-coordinate of point P is:

`x_P=x_U-4=6-4=2_{}_{}`

The vertical distance between points U and T is:

`y_T-y_U=-2-(-10)=-2+10=8_{}`

So the y-coordinate of point P is:

`y_P=y_U+8=-2+8=6`

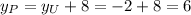
Therefore the coordinates of point P are (2, 6)

b. The length of a segment with endpoints (x1, y1) and (x2, y2) is:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

In this case the endpoints are P (2, 6) and T (10, -10). The length of the segment is:

`\begin{gathered} d=\sqrt[]{(10-2)^2+(-10-6)^2} \\ d=\sqrt[]{8^2+16^2} \\ d=\sqrt[]{64+256} \\ d=\sqrt[]{320} \\ d=8\sqrt[]{5} \end{gathered}`

c. The slope between two points (x1, y1) and (x2, y2) is:

`m=(y_1-y_2)/(x_1-x_2)`

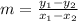
In this case the points we can use are P and T, or P and U or U and T. This is because they are all collinear, so between each pair of points the slope is the same. We'll use points P(2, 6) and T(10, -10):

`m=(-10-6)/(10-2)=(-16)/(8)=-2`

The slope is -2.

d. First we have to find the equation of the line with the segment PT. It has the form:

`y=mx+b`

We have m, which is the slope and we need b, which is the y-intercept. The equation we have for now is:

`y=-2x+b`

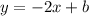
To find b we just have to replace (x, y) by any point on the line and solve for b. Using point U(6, -2):

`\begin{gathered} -2=-2\cdot6+b \\ -2=-12+b \\ b=12-2 \\ b=10 \end{gathered}`

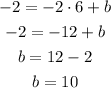
The equation of the line with segment PT is:

`y=-2x+10`

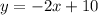
But we have to find the equation of a parallel line to this one. This is very easy now, because parallel lines have the same slope, but different y-intercept. Hence, the equation of a parallel line would be the same equation changing the y-intercept 10 by any arbitrary value. Let's say the y-intercept is 2, so a parallel line is:

`y=-2x+2`