Darnell is building a triangular community garden plot.
Which set of lengths can be used to create the plot perimeter?
Recall the triangle inequality theorem which states that the sum of any two sides must be greater than the third side.
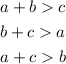
Let us analyze each of the given options.
Option A:
a = 20 feet
b = 12 feet
c = 34 feet

Option B:
a = 8 feet
b = 10 feet
c = 19 feet
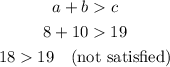
Option C:
a = 5 feet
b = 8 feet
c = 14 feet

Option D:
a = 12, feet
b = 14 feet
c = 20 feet
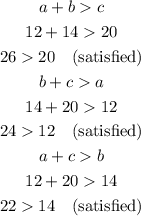
As you can see, only option D satisfies the triangle inequality theorem
Therefore, option D is the correct answer.