The rule of the compounded continuously interest is
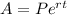
The rule of the compounded monthly interest is

A is the new amount
P is the initial amount
r is the rate in decimal
t is the time in years
Since the initial amount is $100, then
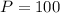
Since the interest rate is 8%, then
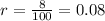
Since the time is from 8 years old to 15 years old, then

a)
Substitute these values in the second rule above
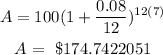
You will receive about $174.74
b)
Substitute these values in the first rule
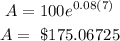
You will receive about $175.07