Question

Solve the following system of linear equations by choosing either substitution or elimination.

Answer 1

To solve the given system of linear equations.

For elimination method:

1. Turn the equations to get that one of the terms with variables be opposite. In this case you can multiply one of the equation for -1:

Multiply the first equation for -1:

`\begin{gathered} -1(4x+3y=-28) \\ -4x-3y=28 \end{gathered}`

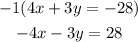
2. Add both equations:

3. Solve y in the result of the addition in step 2:

`-12y=48`

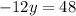
Divide both sides of the eqution into -12

`\begin{gathered} (-12)/(-12)y=(48)/(-12) \\ \\ y=-4 \end{gathered}`

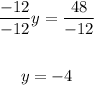
4. Use the value of y= -4 to find the value of x:

Substitute in one of the equations the y for -4 and solve for x:

`\begin{gathered} 4x+3y=-28 \\ 4x+3(-4)=-28 \\ 4x-12=-28 \end{gathered}`

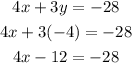
Add 12 in both sides of the equation:

`\begin{gathered} 4x-12+12=-28+12 \\ 4x=-16 \end{gathered}`

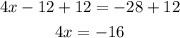
Divide both sides of the equation into 4:

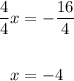
`\begin{gathered} (4)/(4)x=-(16)/(4) \\ \\ x=-4 \end{gathered}`Then, the solution for the system is ( -4, -4)