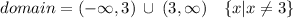Question

Find the Domain f(x)=2x-1/x-3

Answer 1

We are given the following function

`f(x)=(2x-1)/(x-3)`

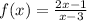
We are asked to find the domain of this function.

Domain:

The domain is all the possible values of input (x) for which the function is defined.

For the given case, notice that when x = 3, the denominator becomes 0 and hence the function is undefined.

So, the possible values of x are from negative infinity to less than 3 and greater than 3 to positive infinity (excluding 3)

Therefore, the domain of the function is

`domain=(-\infty,3)\: \cup\: (3,\infty)\quad \mleft\lbrace x\mright|x\\e3\}`