Question

A bomber is flying at a height of 3.6 km at a speed of 803 km/hr. How far in front of the target should hedrop his bombs? (HINT: the acceleration due to gravity in km/hr is 127,138 km/hr.)

Answer 1

The given problem can be exemplified in the following diagram:

We are given that a plane is traveling at a horizontal speed of 803 km/h at a height of 3.6 km and that it drops a bomb. Due to inertia, the falling bomb will describe a parabolic movement, therefore we can use the equations of motion associated with parabolic movement in order to determine the value of "x". First, we will calculate the time it takes the bomb to fall all the way to the ground. To do that we will use the following formula:

`y=v_(0y)t+(1)/(2)gt^2`

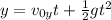
Where:

`\begin{gathered} v_(0y)=\text{ speed in the vertical direction} \\ t=\text{ time} \\ g=\text{ acceleration of gravity} \end{gathered}`

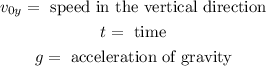
Since the plane is moving horizontally, the speed in the vertical direction is zero. Therefore, the equation reduces to:

`y=(1)/(2)gt^2`

Now we solve for "t" first by multiplying both sides by 2:

`2y=gt^2`

Now we divide both sides by "g":

`(2y)/(g)=t^2`

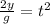
Now we take the square root to both sides:

`\sqrt[]{(2y)/(g)}=t`

Now we replace the given values:

Solving the operations we get:

`0.0075h=t`

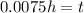
Now that we have the value of the time we can use the following equation for the value of "x":

`x=v_(0x)t`

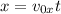
Where:

`v_(0x)=\text{speed in the horizontal direction}`

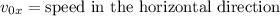
The speed in the horizontal direction is the speed of the plane. Replacing the values we get:

Solving the operations we get:

Therefore, the plane must drop the bomb at 6.04 kilometers in front of the target.