The point-slope form of the line is:
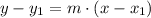
Where m is the slope and the line passes through the point (x1, y1)
Given: the slope = m = -2
And the line passes through the point (-8,-1)
Substitute with the slope and the point into the equation of the line:
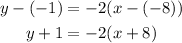
Solve the equation for y to get the slope-intercept form
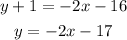
So, the answer will be:
point-slope form ⇒ y+1 = -2(x+8)
slope-intercept form ⇒ y = -2x - 17