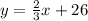It is a question for linear equation
Let the number of donuts be y and the time be x
Since she can make 30 donuts from 8:15 to 9:00
We will find how many minutes from 8:15 to 9:00
There are 45 minutes from 8:15 to 9:00
Then the first point is (45, 30)
We need to find how many donuts she can make from 7:35 to 8:15
Since there are 25 minutes from 7:35 to 8:00
Since there are 15 minutes from 8:00 to 8:15, then
There are 25 + 15 = 40 minutes from 7:35 to 8:15
By using the proportional way we can find the number of donuts
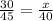
By using the cross multiplication
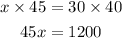
Divide both sides by 45
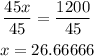
Then she can finish 26 donuts before 8:15
b.
The form of the slope-intercept form is

m is the slope
b is the y-intercept (initial amount)
Since she will start counting from 8:15
Then the initial amount will be the 26 donuts
b = 26
The slope will be the ratio between the number of donuts and the time

The equation is