Question

The approximate mean age is years.(Round to one decimal place as needed.)Approximate the mean of the frequency distribution for the ages of the residents of a town.Age0-910-1920-2930-3940-4950-5960-6970-7980-89Frequency32351228246043173

Answer 1

To calculate the mean value of a data set displayed on a frequency table you have to use the following formula:

`X_{\text{bar}}=(\Sigma x^(\prime)fi)/(n)`

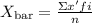
Where

Xbar is the mean value

x' is the classmark (or midpoint) of each interval

fi is the observed frequency of each interval

n is the sample size.

To determine the sample size you have to add the observed frequencies of all intervals:

`\begin{gathered} n=\Sigma fi \\ n=32+35+12+28+24+60+43+17+3 \\ n=254 \end{gathered}`

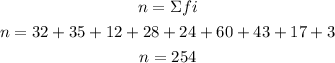
To determine the classmark of each interval you have to add the upper bond and the lower bond and divide it by 2

`x^(\prime)=\frac{\text{upperbond}+\text{lowerbond}}{2}`

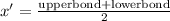
First interval (0-9)

`\begin{gathered} x^(\prime)=(9+0)/(2) \\ x^(\prime)=4.5 \end{gathered}`

Second interval (10-19)

`\begin{gathered} x^(\prime)=(19+10)/(2) \\ x^(\prime)=14.5 \end{gathered}`

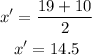
Third interval (20-29)

`\begin{gathered} x^(\prime)=(29+20)/(2) \\ x^(\prime)=24.5 \end{gathered}`

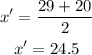
Fourth interval (30-39)

`\begin{gathered} x^(\prime)=(30+39)/(2) \\ x^(\prime)=34.5 \end{gathered}`

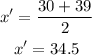
Fifth interval (40-49)

`\begin{gathered} x^(\prime)=(49+40)/(2) \\ x^(\prime)=44.5 \end{gathered}`

Sixth interval (50-59)

`\begin{gathered} x^(\prime)=(59+50)/(2) \\ x^(\prime)=54.5 \end{gathered}`

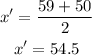
Seventh interval (60-69)

`\begin{gathered} x^(\prime)=(69+60)/(2) \\ x^(\prime)=64.5 \end{gathered}`

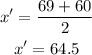
Eighth interval (70-79)

`\begin{gathered} x^(\prime)=(79+70)/(2) \\ x^(\prime)=74.5 \end{gathered}`

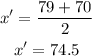
Ninth interval (80-89)

`\begin{gathered} x^(\prime)=(89+80)/(2) \\ x^(\prime)=84.5 \end{gathered}`

Next is to multiply each classmark by the frequency of the corresponding interval:

Once you've multiplied each classmark by each frequency and added all results, you can calculate the mean value using the formula:

`\begin{gathered} X_{\text{bar}}=(∑x^(\prime)fi)/(n) \\ X_{\text{bar}}=(10543)/(254) \\ X_{\text{bar}}=41.507\approx41.5 \end{gathered}`

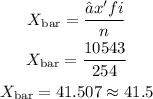
The average or mean age of the resident of the town is 41.5 years