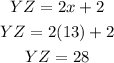We are given two similar triangles, that means that their corresponding sides are at the same proportion with each other, that is:
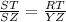
Where:
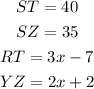
Replacing the known values, we get:
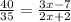
Now we will solve for "x". First by simplifying the fraction on the left:
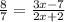
Now we multiply both sides by (2x+2):
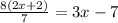
Now we multiply both sides by 7:
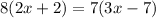
Now we solve the parenthesis:
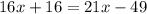
Now we subtract 21x on both sides:
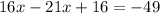
Now we subtract 16 on both sides:
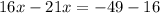
Solving the operations:
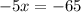
Now we divide both sides by -5
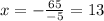
Therefore, the value of x is 13. Now we replace in the equations for the segments, like this:
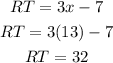
For the other segment: