Question

H varies directly as L. If H = 15 when L = 30, determine H when L = 20A. Write the variation of the equation.B. Determine the value of the quantity indicated.

Answer 1

A. The variation of the equation is

`H=(1)/(2)L`

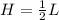
B. H is 10 when L is 20

Step-by-step explanation:

Given that H varies directly as L, this can be written as:

`H\propto L`

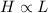
and defined as:

`H=kL`

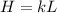
where k is constant.

To find the value of k, we use the given values H = 15 when L = 30

`15=30k`

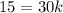
Divide both sides by 30

A.

`k=(15)/(30)=(1)/(2)`

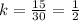
Therefore, the formula is:

`H=(1)/(2)L`

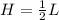
B.

We want to determine H when L is 20

`H=(1)/(2)(20)=10`

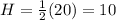
H is 10 when L is 20