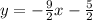ANSWER
Step-by-step explanation
Two lines are perpendicular if their slopes are opposite reciprocals of each other.
In this case, we can rewrite the equation of the given line in slope-intercept form by solving the equation for y,
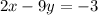
Add 9y to both sides,
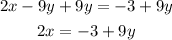
Add 3 to both sides,
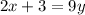
And divide both sides by 9,
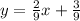
As we can see, the slope of the given line is 2/9. Its opposite reciprocal is -9/2. This is the slope of the line we have to find,
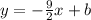
To find the y-intercept, b, we have to use the point (-1, 2). Replace x and y with the coordinates of the point,
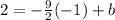
And solve for b,
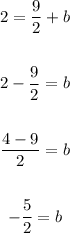
Hence, the equation of the line is,