Question

Type the correct answer in each box. If necessary, use / for the fraction bar. Find the solution to this system of equations. Ity = 1 21-y+z = 1 1+2y+z IL y = = Reset Next

Answer 1

• x = 1/3

,

• y = 2/3

,

• z = 1

Step-by-step explanation

There are many methods to solve a linear system of equations, but in this case we have to use the substitution method -which consists in clearing one variable as a function of the other/s and replace in another equation. For a system of three variables such as this one, we have to do this twice:

1° clear x from the first equation:

`\begin{gathered} x+y=1 \\ x=1-y \end{gathered}`

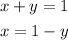
Replace x by this expression in the second equation:

`\begin{gathered} 2x-y+z=1 \\ 2(1-y)-y+z=1 \end{gathered}`

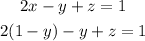
Note that now we have two variables, y and z. Before the next step we have to rewrite the equation above so that we only have one y:

`\begin{gathered} 2\cdot1-2y-y+z=1 \\ 2-3y+z=1 \end{gathered}`

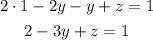
2° clear y from the equation above:

`\begin{gathered} -3y+z=1-2 \\ -3y=-1-z \\ y=(-(1+z))/(3) \\ y=(1+z)/(3) \end{gathered}`

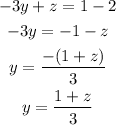
And replace y by this expression in the last equation. Note that the third equation also contains x, so we have to replace first x as a function of y like in the first step:

`\begin{gathered} x+2y+z=(8)/(3) \\ (1-y)+2y+z=(8)/(3) \end{gathered}`

Rewrite it so we only se one y:

`\begin{gathered} 1-y+2y+z=(8)/(3) \\ 1+y+z=(8)/(3) \end{gathered}`

And now we replace y by the expression we found in the second step:

`1+(1+z)/(3)+z=(8)/(3)`

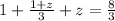
So now we have one equation with one variable. Let's solve for z:

`\begin{gathered} 1+(1)/(3)+(z)/(3)+z=(8)/(3) \\ (4)/(3)+(4z)/(3)=(8)/(3) \\ (4z)/(3)=(8)/(3)-(4)/(3) \\ (4z)/(3)=(4)/(3) \\ z=1 \end{gathered}`

We have that z = 1.

The next steps are to back replace and find the other variables. Remember that in the second step we had y as a function of z:

`y=(1+z)/(3)`

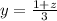
Replace z = 1 and solve:

`y=(1+1)/(3)=(2)/(3)`

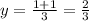
y = 2/3

And finally, replace y = 2/3 in the expression of the first step, where we found x as a function of y:

`x=1-y=1-(2)/(3)=(1)/(3)`

and we got x = 1/3