The proof uses basic properties and definitions from geometry, including bisectors, perpendicular lines, reflexive property, and congruence postulates such as Right Angle Hypotenuse Side (RHS) and CPCTC.
The problem provided is a geometric proof involving triangle bisectors. The goal is to prove that XY is congruent to ZY, given that
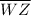 is the perpendicular bisector of
is the perpendicular bisector of
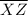 . Here's how to fill out the missing statements and reasons in the proof:
. Here's how to fill out the missing statements and reasons in the proof:
1. W is perpendicular to XZ, WZ bisects XZ
2. XW is congruent to ZW
- Reason: Definition of a bisector (a bisector divides a segment into two equal parts)
3.
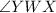 and
and
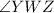 are right angles, so
are right angles, so
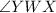 is congruent to
is congruent to
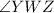 .
.
- Reason: Definition of perpendicular (a perpendicular line forms right angles)
4. YW is congruent to YW
- Reason: Reflexive property (a segment is always congruent to itself)
5.
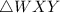 is congruent to
is congruent to
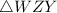
- Reason: Right Angle Hypotenuse Side (RHS) Congruence (if the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and leg of another right triangle, the triangles are congruent)
6. XY is congruent to ZY
- Reason: Corresponding parts of congruent triangles are congruent (CPCTC)