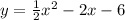Question

Write the equation of the quadratic function in standard form given the roots are 6 and -2 and a point on the graph is (10,24)

Answer 1

Step-by-step explanation

Since we have that the roots are (6,0) and (-2,0) and a point on the graph, the canonical quadratic equation is as follows:

`y=a(x-6)(x-(-2))`

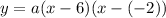
Subtracting:

`y=a(x-6)(x+2)`

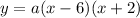
Applying the distributive property:

`y=a(x^2+2x-6x-12)`

Adding like terms:

`y=a(x^2-4x-12)`

Now, in order to compute the value of a, we must plug the point (10,24):

`24=a(10^2-4\cdot10-12)`

Multiplying numbers:

`24=a(100-40-12)`

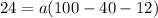
Adding numbers:

`24=a(48)`

Dividing both sides by 48:

`(24)/(48)=a`

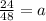
Simplifying:

`(1)/(2)=a`

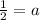
Switching sides:

`a=(1)/(2)`

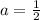
Plugging in a into the equation:

`y=(1)/(2)(x^2-4x-12)`

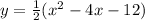
Applying the distributive property:

`y=(1)/(2)x^2-2x-6`

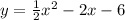
In conclusion, the expression of the quadratic equation is as follows:

`y=(1)/(2)x^2-2x-6`