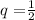Solution:
The given equation is:
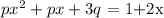
We can write it as:
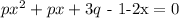
Rearrange the terms, we get:
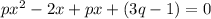
This can be written as:

Now wrt Standard form of a quadratic equation:

we have:
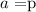
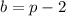
and
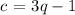
We know that product of zeroes :
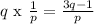
then
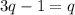
then
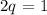
so that,
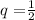
Sum of roots :
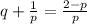
then
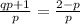
then
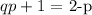
then
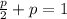
solving for p, we get:
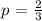
so that, we can conclude that the correct answer is:
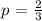
and