Question

Maria loves the lunch combinations at Diner's Delite. Today, however, she wants adifferent combination than the ones listed on the menu.Two burgers, one french fries $7.55One coke, one burger, one french fries $8.10Two cokes, two burgers $9.90Assume that the price of a combo meal is the same price as purchasing each itemseparately. Find the price for a burger, a coke, and french fries.burger $2.20 french fries S3 15. coke S2.75burger: S3 15. french fries $2.20, coke S2.75burger $1.20, french fries: $3.15 coke: $3.75burger $2.78, french fries: S3 10 coke S2.22

Answer 1

Let b be the price of the burger, c the price of the coke, and f the price of the french fries, then we can set the following system of equations:

`\begin{gathered} 2b+f=7.55, \\ b+c+f=8.10, \\ 2c+2b=9.90. \end{gathered}`

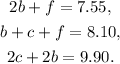
Subtracting the second equation from the first one we get:

`b-c=7.55-8.10=-0.55.`

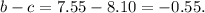
Now, subtracting the two times the above equation from the third equation we get:

`\begin{gathered} 2c+2b-2b+2c=9.90-2(-0.55), \\ 4c=11, \\ c=(11)/(4)=2.75\text{.} \end{gathered}`

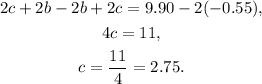
Substituting c=2.75 in the third equation and solving for b we get:

`\begin{gathered} 2(2.75)+2b=9.90, \\ 2b=9.90-5.5=4.4, \\ b=2.2\text{.} \end{gathered}`

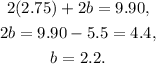
Finally, substituting b=2.2 in the first equation and solving for f we get:

`\begin{gathered} 2(2.2)+f=7.55, \\ f=7.55-4.4=3.15\text{.} \end{gathered}`

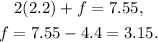
Answer: The burger costs $2.20, the price of the french fries is $3.15, and the price of the coke is $2.75.