Given the Quadratic Function:
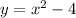
You need to remember that the Quadratic Parent Function (the simplest form of a Quadratic Functions) is:
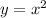
And its vertex is at the Origin:

The function given in the exercise was obtained by shifting the parent function 4 units down. That means that the y-coordinate of the vertex changes, but the x-coordinate is the same. Therefore, the vertex of this parabola is:
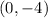
To find two points to the left of the vertex, you can choose this value for "x":

Substituting this value into the function and evaluating, you can find the corresponding value of "y":
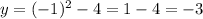
Now you have this point:

You can choose this value of "x":
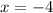
And apply the same procedure:
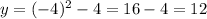
Then, the other point is:
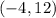
To find the first point to the right of the vertex, you can substitute this value of "x" into the function and evaluate:
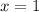
Then, you get:

The point is:
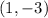
To find the second point, substitute this value into the equation and evaluate:

Then:
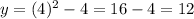
So the other point is:
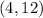
Now you can plot the points and graph the function.
Therefore, the answer is: