In order to find the interior angles of the green triangle, first let's find the angle CAB in the upper blue triangle, using its tangent relation:
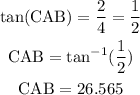
Since the figure is symmetrical, angle FAE is also 26.565° and triangle AEC is isosceles.
Now, we can find angle CAE:
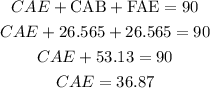
Finding angles ECA and AEC:
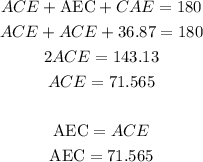
In order to calculate the area of green triangle, we can first calculate the length of all three sides using Pythagorean theorem:
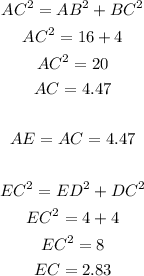
So the area of the triangle using Heron's formula is:
![\begin{gathered} A=\sqrt[]{p(p-a)(p-b)(p-c)} \\ p=(4.47+4.47+2.83)/(2)=5.885 \\ A=\sqrt[]{5.885(1.415)\mleft(1.415\mright)\mleft(3.055\mright)} \\ A=6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k7cp83pbouq6q2c7km6qlwj5ol0dd4opdj.png)
So the area of the triangle 6 mm².