Given that the downward weight, mg = 800 N and tension in the swing is, T = 1040 N.
Also centripetal force,
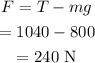
Mass of the swing can be obtained using the weight
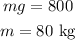
Here, g = 10 m/s^2 is the acceleration due to gravity.
Centripetal force can also be written as
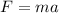
Here, a is the Centripetal acceleration.
Thus, centripetal acceleration is
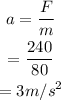
Hence the child's centripetal acceleration is 3 m/s^2