Step-by-step explanation
Calculus / Limit
In this problem, we must find the end behaviour of y as x tends to infinity in the equation:
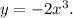
• Taking the limit for x → -∞, we have:
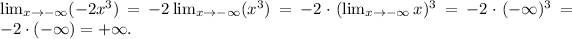
• Taking the limit for x → +∞, we have:
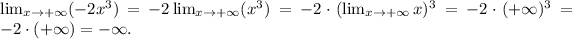
Answer
• When x → -∞, the function y tends to +∞
• When x → +∞, the function y tends to -∞