Question

Start by proving the first identity, sinh (x + y)= sinh x cosh y + cosh x sinh y. Use the fact that sinh x = e^x - e^~x/2 to rewrite the left side, sinh (x + y), using exponentials. Sinh (x+y) =

Answer 1

The formula for sinh x in exponential form is,

`\sinh x=(e^x-e^(-x))/(2)`

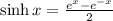
Substitute x + y for x in formula to determine the eponential expression for sinh (x + y).

`\sinh (x+y)=(e^(x+y)-e^(-(x+y)))/(2)`

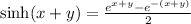
Simplify the exponential expression of sinh (x + y) to prove the identity.

`\begin{gathered} (e^(x+y)-e^(-(x+y)))/(2)=(2e^(x+y)-2e^(-x-y))/(4) \\ =(2e^(x+y)+(e^(x-y)-e^(y-x))-(e^(x-y)-e^(y-x))-2e^(-x-y))/(4) \\ =((e^(x+y)+e^(x-y)-e^(-x-y)-e^(y-x))+(e^(x+y)-e^(x-y)+e^(-x-y)-e^(y-x)))/(4) \\ =(e^(x+y)+e^(x-y)-e^(-x-y)-e^(y-x))/(4)+(e^(x+y)-e^(x-y)+e^(-x-y)-e^(y-x))/(4) \\ =(e^x(e^y+e^(-y))-e^(-x)(e^(-y)+e^y))/(4)+(e^x(e^y-e^(-y))+e^(-x)(e^(-y)-e^y))/(4) \\ =((e^y+e^(-y))/(2))((e^x-e^(-x))/(2))+((e^y-e^(-y))/(2))((e^x+e^(-x))/(2)) \\ =\cosh y\sinh x+\sinh y\cosh x \end{gathered}`

Hence it is proved that,

sinh (x + y) = sinh x cosh y + sinh y cosh x