Question

Determine the surface area of a square based pyramid that has a slant height of 13.6 mand a base length of 4.8 m? Round your answer to the nearest whole.

Answer 1

A square-based pyramid comprises of a square base and 4 triangular faces too

Therefore,

The surface area of a square-based pyramid is calculated as

`\begin{gathered} S\mathrm{}A=\text{Area of square+ area of 4 tiriangular faces} \\ S\mathrm{}A=l^2+4((1)/(2)* base* height) \\ \text{where,} \\ l=4.8m \\ \text{base}=4.8m \\ \text{height of the triangle=13.6m} \end{gathered}`

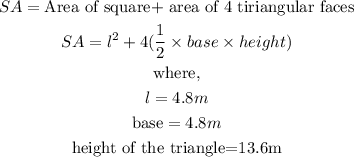
By substitution,

`\begin{gathered} S\mathrm{}A=(4.8m)^2+4((1)/(2)*4.8m*13.6m) \\ S\mathrm{}A=23.04m^2+4((65.28m^2)/(2)) \\ S\mathrm{}A=23.04m^2+4(32.64m^2) \\ S\mathrm{}A=23.04m^2+130.56m^2 \\ S\mathrm{}A=153.6m^2 \\ to\text{ the nearest whole number} \\ S\mathrm{}A=154m^2 \end{gathered}`

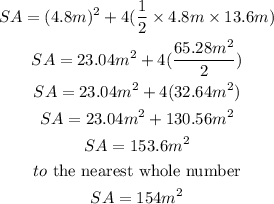
Hence,

The surface area of the square-based pyramid to the nearest whole number is 154m²