A square-based pyramid comprises of a square base and 4 triangular faces too
Therefore,
The surface area of a square-based pyramid is calculated as
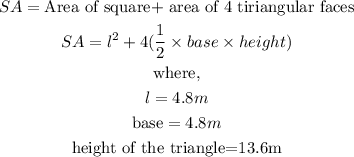
By substitution,
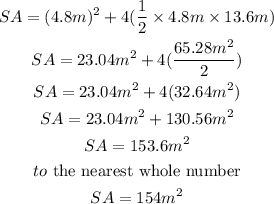
Hence,
The surface area of the square-based pyramid to the nearest whole number is 154m²