To solve this, we'll use Euler's Polyhedral formula.
This formula states that in any polyhedron, the number of vertices V, faces F, and edges E, satisfy:
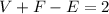
If we solve for the edges E, we'll get:
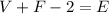
Using the data given,
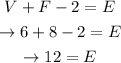
We get that the polyhedron would have 12 edges