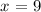Question:
Solution:
Consider the following function:

where x is measure in seconds and h(x) represents the height of the object. Now, if the hovercraft land on the ground then h(x) = 0. Thus, we get:

Our goal is to solve this for x. Expanding the square we have that the above equation is equivalent to:
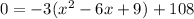
applying the distributive property we obtain:
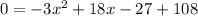
this is equivalent to:

or

Using the quadratic formula we obtain that the solutions of this equation are:
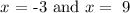
Note that by convention time is positive, therefore the correct answer is