Question

The sum of two numbers is 24. Find the maximum value of their product.

Answer 1

Let x and y be the two numbers we are looking for. We are told that the sum is 24. So we have the equation

`x+y=24`

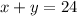
we want to calculate the maximum value of the product of both numbers, that is

`x\cdot y`

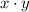
From the first equation we could replace the value of y, so we have that

`x(24\text{ -x\rparen=24x- x}^2`

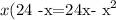
which is a parabolla. Recall that the general form of a parabolla is given by the equation

`y=a(x\text{ -h\rparen}^2+k`

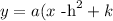
where (h,k) is the vertex of the parabolla. In this case, k would be the maximum or minimum value of the parabolla.

We start by factoring out the -1. So we get

`y=\text{ - \lparen x}^2\text{ -24x\rparen}`

now, we will complete the square inside the parentheses. Note that if

`(a\text{ -b\rparen}^2=a^2\text{ - 2ab + b}^2`

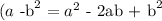
and we let a = x we have that

`(x\text{ -b\rparen}^2=x^2\text{ -2bx+b}^2`

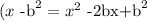
If we compare this to the expression x^2 -24x, we can see that -2b=-24. So we have

`\begin{gathered} \text{ -2b= -24} \\ b=\frac{\text{ -24}}{\placeholder{⬚}\text{ -2}} \\ b=12 \end{gathered}`

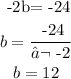
So, we will add and subtract 12² so we get

`y=\text{ -\lparen x}^2\text{ -24x+12}^2\text{ -12}^2)=\text{ -\lparen x}^2\text{ -24x+12}^2)\text{ +12}^2`

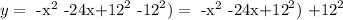
which is equivalent to

`y=\text{ -\lparen x -12\rparen}^2+12^2`

by comparison, we can see that in here the value of k is 12^2. THat is

`k=12^2=144`

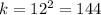
which is the maximum value of the product. So the correction option is the third option.