Given:
The initial temperatures of the liquids 1,2 and 3 are

the final temperature of the first two liquids is
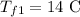
the final temperature of the second and third liquids is
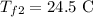
Required:
final temperature of the first and third liquidd.
Step-by-step explanation:
to solve this problem apply principal of calorimetry here,
for the first two liquids is
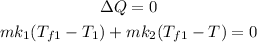
plugging all the values in the above relation we get

here k1 nad k2 are the specific heat of the two liquids
now similarly for, second and third liquids
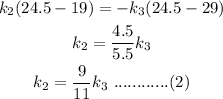
here, k3 is specific heat of liquid three
from the equation (1) and (2) we can write
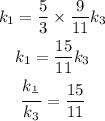
now for liquid first and third
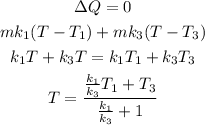
Plugging all the values in the above relation we get
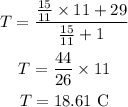
Thus, the final equilibrium temperature is
