Question

Find the value of x. A. 241−−√ inB. 53–√ inC. 9D. 55–√ in

Answer 1

We have the following right triangle:

And we need to find the measure of the side represented by x.

To find it, we can proceed as follows:

1. Apply the Pythagorean Theorem as follows:

`x^2+(5in)^2=(10in)^2`

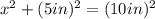
We have that the sum of the squares of the legs (5 in and x inches) of the right triangle is equal to the square of the hypotenuse (10 in).

2. Then subtract (5in)^2 from both sides of the equation:

`\begin{gathered} x^2+(5in)^2-(5in)^2=(10in)^2-(5in)^2 \\ \\ x^2=(10\text{in})^2-(5\text{in})^2 \end{gathered}`

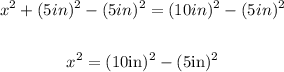
3. Now, we can extract the square root to both sides of the equation (without using units):

`\begin{gathered} √(x^2)=√(100-25)=√(75) \\ \\ x^=√(75) \end{gathered}`

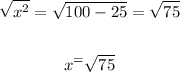
4. Finally, to simplify the number at the right of the equation, we can factor the radicand as follows:

And these are the prime factors for 75. Then we can rewrite the value as follows:

`\begin{gathered} 75=3*5^2 \\ \\ x=√(75)=√(3*5^2)=5√(3) \\ \\ x=5√(3) \end{gathered}`

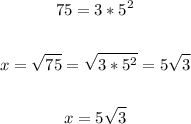
Therefore, in summary, the value for x is:

`x=5√(3)\text{ in}`

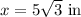
[Option B.]