Use Newton's Law of Universal Gravitation to find the gravitational force (which is the same as the weight) that a 68.0 kg person feels due to the interaction with Earth.
The force between two bodies with masses M and m separated by a distance r is:
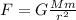
Where G is the gravitational constant:
![G=6.67*10^(-11)N\frac{m^2}{\operatorname{kg}^2}]()
Use M=5.97*10^24kg for the mass of the Earth, and R=6.371*10^6m for the radius of the Earth.
A)
For a person situated on the surface of the Earth, we can consider it to be situated at a distance equal to the radius of the Earth from all its mass. Then:
![\begin{gathered} F=(6.67*10^(-11)N\frac{m^2}{\operatorname{kg}^2})*\frac{(5.97*10^(24)\operatorname{kg})(68.0\operatorname{kg})}{(6.371*10^6m)^2} \\ =667N \end{gathered}]()
B)
For a person situated 8,848 meters above the sea level, add 8,848m to the radius of the Earth in the formula:
![\begin{gathered} F=(6.67*10^(-11)N\frac{m^2}{\operatorname{kg}^2})*\frac{(5.97*10^(24)\operatorname{kg})(68.0\operatorname{kg})}{(6.371*10^6m+8848m)^2} \\ =665N \end{gathered}]()
C)
For a person situated at 2.5 times the radius of the Earth from its center, multiply the radius of the earth by 2.5 in the formula:
![\begin{gathered} F=(6.67*10^(-11)N\frac{m^2}{\operatorname{kg}^2})*\frac{(5.97*10^(24)\operatorname{kg})(68.0\operatorname{kg})}{(2.5*6.371*10^6m)^2} \\ =107N \end{gathered}]()