Question

Identify the similar triangles. then find each measure. EG, HG.

Answer 1

Hello!

First, notice that as we have similar sides, we will also have similar sides. So:

EF is similar to HI

EG is similar to GH

FG is similar to GI

Notice that we know the measurement of four sides, so we can write it as a proportion, look:

`(EF)/(HI)=(EG)/(GH)`

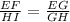
Replacing with the values:

`(3)/(4)=(x+1)/(x+3)`

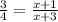
Multiplying it across:

`\begin{gathered} 3\cdot(x+3)=4(x+1) \\ 3x+9=4x+4 \\ 9-4=4x-3x \\ 5=x \\ x=5 \end{gathered}`

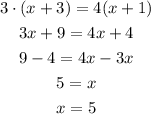
Now, let's replace it to know the measurement of sides with unknowns (EG and GH):

`\begin{gathered} EG=x+1 \\ EG=5+1 \\ EG=6 \\ \\ GH=x+3 \\ GH=5+3 \\ GH=8 \end{gathered}`

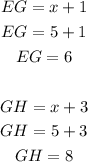
Right answer: third alternative.