Step-by-step explanation:
The end behavior of a polynomial is a description of what happens as x becomes large in the positive or negative direction. Now, to describe end behavior, it is used the following notation:
x → ∞ : “x becomes large in the positive direction”
x → -∞ : “x becomes large in the negative direction”
analogously for the variable "y".
A constant function is a polynomial of degree 0. When f(x) = c, any value selected for x will yield c for the y-value. The graph of a constant function will be a horizontal line intersecting the y-axis at the value of c.
Thus, consider the following function constant function:
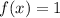
The graph for this function is:
According to the graph of this function, we can see that the end behavior will be:
Notice that this function is a constant function and it can be a sinusoidal function since a sinusoidal function is a curve, referred to as a sine wave or a sinusoid, that exhibits smooth, periodic oscillation, and this is not the case of a constant function where the value of y will not oscillate but will remain constant.
Finally, the zeros of a function are the x-coordinates where the function crosses the x-axis. That is x-intercepts. As we can see in the graph of the function f(x)=1, this graph never intersects the x-axis so it has no zeros.
We can conclude that the correct answer is:
Answer:
A) End behavior:
y → 1 as x → ∞
and
y → 1 as x → -∞
B) Is it a sinusoidal function?
The given constant function is not a sinusoidal function.
C) Does this function have zeros?
The given constant function has no zeros.