Question

1 (a) Solve each system by graphing. If there is no solution or an infinite number of solutions, so state. use set notation to express solution sets.

Answer 1

We want to find the solution(s) for two systems.

item (a):

In the first item, we have

`\begin{cases}y=2x-1 \\ x-2y=-4\end{cases}`

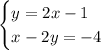
To find the solution of this system, we can just substitute the y-value from the first equation in the second equation, and solve for x.

`\begin{gathered} x-2y=-4 \\ x-2(2x-1)=-4 \\ x-4x+2=-4 \\ -3x=-4-2 \\ -3x=-6 \\ 3x=6 \\ x=2 \end{gathered}`

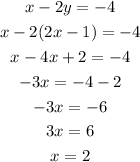
Using this x-value in the first equation, we have

`\begin{gathered} y=2\cdot(2)-1 \\ y=4-1 \\ y=3 \end{gathered}`

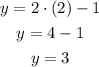
Now, let's check in the second equation if those values fit

`\begin{gathered} x-2y=-4 \\ (2)-2\cdot(3)=-4 \\ 2-2\cdot3=-4 \\ 2-6=-4 \\ -4=-4 \\ 1=1 \end{gathered}`

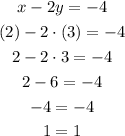
Those values satisfy both equations, therefore, they are the solution for this system. x = 2 and y = 3.

`\lbrace(2,3)\rbrace`

item (b):

On this item we want to solve

`\begin{cases}x+y=5 \\ 2x+2y=6\end{cases}`

We can start by multiplying the first equation by 2.

`\begin{cases}x+y=5 \\ 2x+2y=6\end{cases}=\begin{cases}2(x+y)=2\cdot(5) \\ 2x+2y=6\end{cases}=\begin{cases}2x+2y=10 \\ 2x+2y=6\end{cases}`

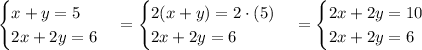
As you can see, we have the same equation on the left side with different values on the right side. This means we have distinct solutions for each equation, this system correspond to a graph of two parallel lines.

Then, we have no solution for this system.

`\lbrace\emptyset\rbrace`