Ok, let's find the side HT to help us decide:
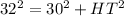
Clearing HT:
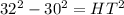
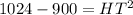
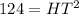
![HT=\sqrt[]{124}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ibfyv041933rznkypzx805vlthq62c9mah.png)
And, now let's find SW:
![\begin{gathered} SW^2=48^2-44^2=2304-1936=368 \\ SW=\sqrt[]{368} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/vcxpr8omg6vubk1gejrrluv7v7owz309e4.png)
And finally let's calculate the angles:
We know that angles T and Q are equal to 90°
M=arccos(30/32)=arccos(0.9375)=20.36
Q=arc cos(44/48)=arccos=23.55
So, finally we have that ΔMTH ~ ΔQWS is similar by SAS.