We have an initial value of $9,900.
We have to model the following situations.
a) The value decreases by 11% per year.
We can start expressing this as:
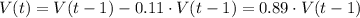
This is a recursive function, as V(t) is function of V(t-1). We can find the explicit function as:
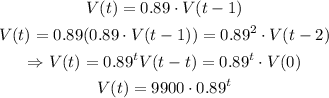
b) The value decreases by $896 per year
This can be modeled as:
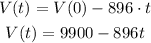
c) The value increases by 6% per year
This will have similarities with the function in the point a).
We can model this as:

d) The value increases by $743 per year
This will be a linear model, as it is the model in point b).
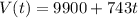
Answer:
a) V = 9900*0.89^t
b) V = 9900 - 896t
c) V = 9900*1.06^t
d) V = 9900 + 743t