Question

camel can compute his school project in x hours. what part of the job can be completed by camel after 3 hours?

Answer 1

Given:

The time taken by the camel to complete the work= x hours.

Let 1 be the total work(W).

So, the work done per hour by the camel(Efficiency) is,

`\begin{gathered} Efficiency(E)=\frac{\text{ Total work(W)}}{\text{Time}} \\ E=(W)/(x) \\ E=(1)/(x) \end{gathered}`

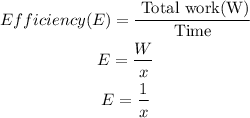
So, the efficiency of camel is 1/x.

Efficiency is a constant.

Since Work =Efficiency x Time taken, the work done by camel in t=3 hours is,

`\begin{gathered} w=E* t \\ =(1)/(x)*3 \\ =(3)/(x) \end{gathered}`

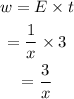
We have to find what part of the of the job can be completed by camel after 3 hours.

Since total work is W=1, the part of the job can be completed by camel after 3 hours is,

`(w)/(W)=((3)/(x))/(1)=(3)/(x)`

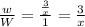
Hence, 3/x part of the job can be completed by camel after 3 hours.