Let:
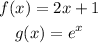
The inverses of each function are:
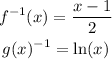
Both:
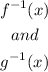
Are functions since for every x:
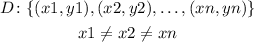
all the inverse of the composite function made by the original function also be a function?.
Yes, since they satisfy the following property:
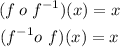
the inverse of the sum or difference of the original function also be a function?
Let's check it out:
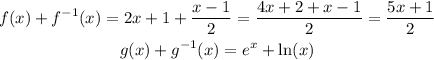
The result for both cases is a function. Therefore, the sum or difference of the original function also will be a function.
From the pic:
The green graph is g(x)
The purple graph is g^-1(x)
The red graph is f(x)
The blue graph is f^-1(x)
The black graph is f(x)+f^-1(x)
The orange graph is g(x)+g^-1(x)
We can verify from the pic that all of them are functions