Question

Please please help!!!

Answer 1

Let:

`\begin{gathered} f(x)=2x+1 \\ g(x)=e^x \end{gathered}`

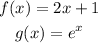
The inverses of each function are:

`\begin{gathered} f^(-1)(x)=(x-1)/(2) \\ g(x)^(-1)=\ln (x) \end{gathered}`

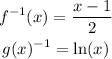
Both:

`\begin{gathered} f^(-1)(x) \\ and \\ g^(-1)(x) \end{gathered}`

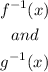
Are functions since for every x:

`\begin{gathered} D\colon\mleft\lbrace(x1,y1\mright),(x2,y2),\ldots,(xn,yn)\} \\ x1\\e x2\\e xn \end{gathered}`

all the inverse of the composite function made by the original function also be a function?.

Yes, since they satisfy the following property:

`\begin{gathered} (f_{\text{ }}o_{\text{ }}f^(-1))(x)=x \\ (f^(-1)_{\text{ }}o_{\text{ }}f^{})(x)=x \end{gathered}`

the inverse of the sum or difference of the original function also be a function?

Let's check it out:

`\begin{gathered} f(x)+f^(-1)(x)=2x+1+(x-1)/(2)=(4x+2+x-1)/(2)=(5x+1)/(2) \\ g(x)+g^(-1)(x)=e^x+\ln (x) \end{gathered}`

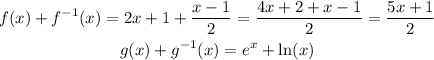
The result for both cases is a function. Therefore, the sum or difference of the original function also will be a function.

From the pic:

The green graph is g(x)

The purple graph is g^-1(x)

The red graph is f(x)

The blue graph is f^-1(x)

The black graph is f(x)+f^-1(x)

The orange graph is g(x)+g^-1(x)

We can verify from the pic that all of them are functions